數據分析和r軟件課后題(R數據分析:變量間的非線性關系，多項式，樣條回歸和可加模型)

之前的文章中都是給大家寫的變量間線性關系的做法，包括回歸和廣義線性回歸，變量間的非線性關系其實是很常見的，今天給大家寫寫如何擬合論文中常見的非線性關系。包括多項式回歸Polynomial regression和樣條回歸Spline regression。

多項式回歸

首先看一個二次項擬合的例子，我現在想探討蘋果內容物apple content和蘋果酸度cider acidity的關系，第一步應該是做出apple content和cider acidity關系的散點圖，假如是下圖：

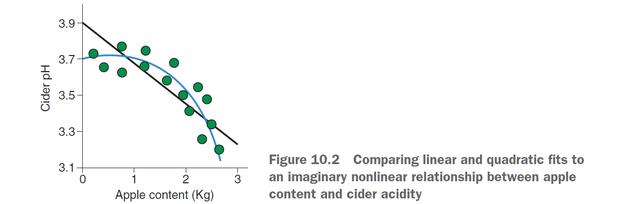
那么我很直觀地可以看出來，曲線（二次）對數據的擬合明顯是好于線性擬合的。

上面的只是一個2次項擬合的例子，我們其實經常會遇到有可能高次式會把數據擬合的更好，社科論文中其實也常常見到做高次回歸的，常見的1次，2次，3次，4次項英文論文中的表達，曲線形狀如下：

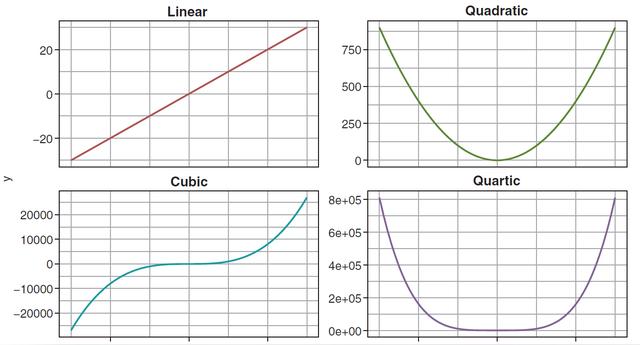
擬合出來的一般模型表達式如下：

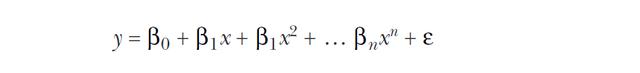
而且通常情況下，模型中所有的低次項都不應該被略去。就是我有了4次項，那么應該3，2，1次項都應該有。

含有二次及以上的模型就叫多項式回歸模型。

樣條回歸

之前在機器學習的文章中有給大家寫過擬合，我們做多次項擬合的時候，按道理你可以將項的次數調得很高，總是可以近乎完美的擬合我們的復雜的非線性關系，但是問題就是外推性就沒有了，這也并不是我們想看到的結果：

High-degree polynomials allow us to capture complicated nonlinear relationships in the data but are therefore more likely to overfit the training set.

還有就是自變量和因變量之間的關系在自變量的不同取值范圍也并非不變的，比如某個區間是線性的，某個區間是2次曲線，某個區間又成了3次曲線。

上面兩個問題處理方法之一就是樣條splines

所謂樣條就是成片段的多次式，一個曲線分多段擬合，段與段之間的分割點叫做結knots

A spline is a piecewise polynomial function. This means it splits the predictor variable into regions and fits a separate polynomial within each region, which regions connect to each other via knots.

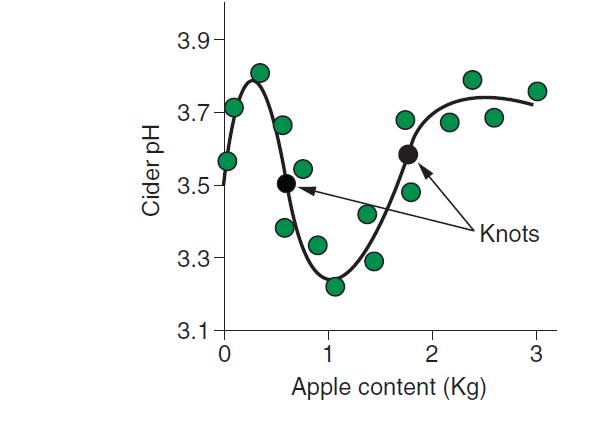
上圖便是用兩個結將我們的曲線分成了3個樣條。

通過對關系曲線的劃分，我們可以盡可能達到既擬合的好，又好解釋的目的。

我們在論文中還會有看到說限制性立方樣條（restricted cubic splines），這個又是個啥呢？

就是我們正常做樣條，有可能做出來就是這樣的：雖然分段但是不連貫：

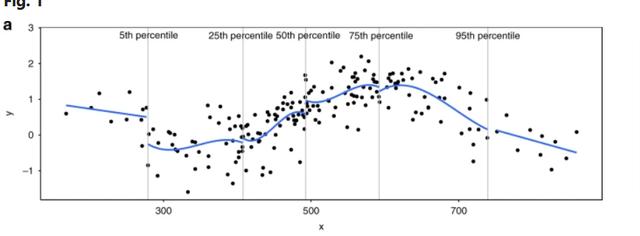
這樣的情況下結點處，不連貫的地方解釋起來就會很困難了嘛。

所以，我們更加期望能夠得到一個平滑的曲線（增加可解釋性），而且首尾都應該是線性的，從而保證預測準確性（減少過擬合的影響），像這樣：

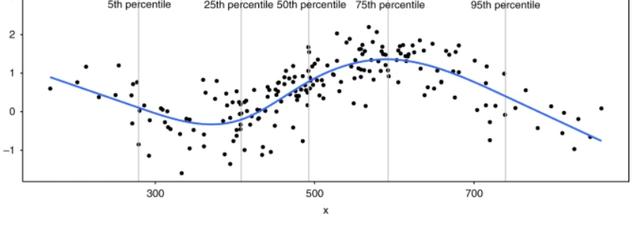
為了得到這么樣的效果我們就會給樣條加上限制，所以叫做限制性立方樣條：

restrictions need to be imposed so that the spline is continuous (i.e., there is no gap in the spline curve) and “smooth” at each knot。A restricted cubic spline has the additional property that the curve is linear before the first knot and after the last knot.

樣條數量的確定和結位置的選擇也是有講究的，結的個數可以自己定，但是一般不超過5個；結的位置需要盡可能在拐彎的地方：

The number of knots used in the spline is determined by the user, but in practice we have found that generally five or fewer knots are sufficient. The location of the knots also needs to be specified by the user, but it is common that the knot with the smallest value is relatively close to the smallest value of the variable being modelled (e.g., the 5th percentile), while the largest knot is in the neighbourhood of the largest value of the variable being modelled (e.g., the 95th percentile).

廣義可加模型

上面寫的內容，無論是直接擬合，還是分段擬合，我們都是在擬合一個完整的曲線或直線方程，廣義可加模型則是將自變量的單獨模型相加，下圖式子即為一般線性模型和可加模型：

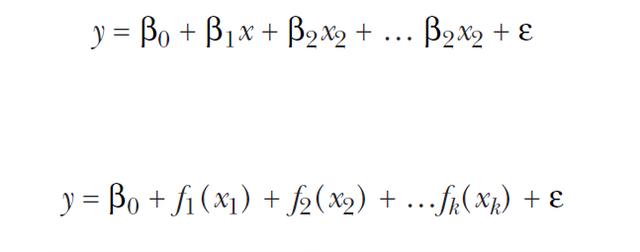
我們看下圖，下圖中對于x和y關系的擬合是通過x的3個基礎函數相加得到的：

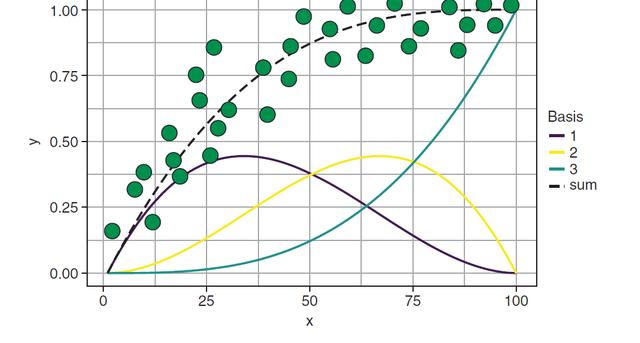
GAMs automatically learn a nonlinear relationship between each predictor variable and the outcome variable, and then add these effects together linearly, along with the intercept.

就是說廣義可加的原理就是，先弄幾個好解釋的基礎函數，這個基礎函數可以是一次的，也可以是多次的，然后再將這些基礎函數進行線性組合，從而達到更好地擬合數據的目的。

通過廣義可加模型可以同時實現模型的可解釋性Interpretability，靈活性flexibility和正則化regularization。

怎么理解呢，我們先看可解釋性，假如一個可加模型是如下形式的基礎函數相加得到的：

x2的作用我們就可以解釋為在其它變量不變的情況下，x2和結局之間的關系是線性的，xp對左邊的結局在某個點之前也基本是線性增加的，然乎某個點之后xp對結局就無影響了，這個就是將模型相加后才可能實現的解釋性。

靈活性在于，可加模型可以將所有自變量單獨建模后相加，我們甚至不需要提前知道xy的關系，完全由數據說話的非參數形式，就比整體的多項式和樣條更靈活。

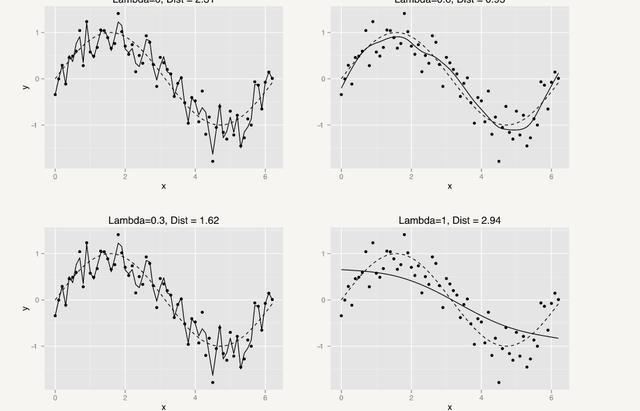
正則化則可以避免過擬合，可加模型是有一個超參λ的，這個超參決定了曲線的歪扭程度，英文叫做wiggliness，通過對超參的控制就可以很方便地實現方差偏差折中，見下圖：

The level of smoothness is determined by the smoothing parameter, which we denote by λ. The higher the value of λ, the smoother the curve

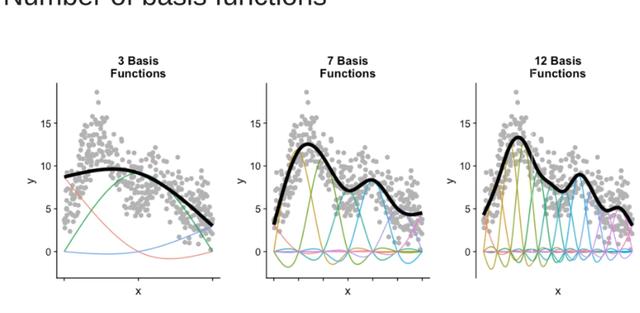
當然還有一個問題就是我到底該用多少個基礎函數呢？基礎函數越多模型就可以越靈活。見下圖，這個大家在具體操作的時候也是可以自己設定的：

實例操練

我現在手上有如下數據

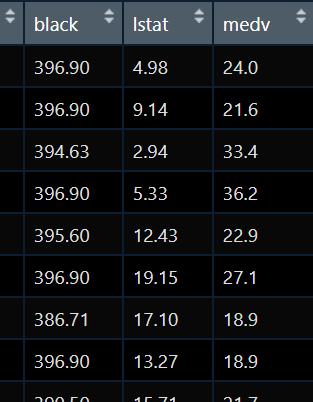
我想探究medv和lstat之間的關系，先做個圖：

ggplot(train.data, aes(lstat, medv) ) +  geom_point() +  stat_smooth()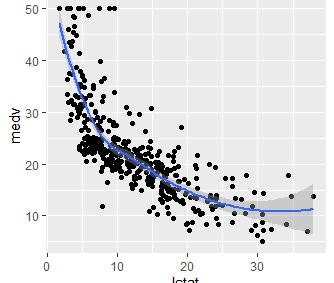

可以看到這兩個變量間是非常明顯的非線性關系，此時我們需要考慮給自變量加上多次項擬合。

在R語言中我們可以使用I()來加上變量的高次項，比如我要加二次項，我就可以寫出I(x^2)

lm(medv ~ lstat + I(lstat^2), data = train.data)

模型結果如下：

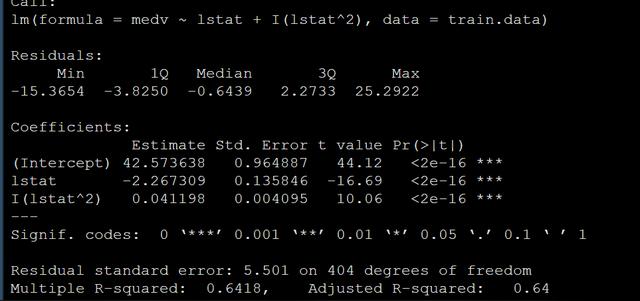
上面就是多次項回歸的做法，接下來給大家寫寫如何做樣條回歸

剛剛有寫我們做樣條的時候是需要設定結的，比如我就設定自變量的第25，50，75百分位為結：

knots <- quantile(train.data$lstat, p = c(0.25, 0.5, 0.75))

做一個立方樣條回歸（默認就是做立方樣條），代碼如下：

model <- lm (medv ~ bs(lstat, knots = knots), data = train.data)

模型輸出結果如下：

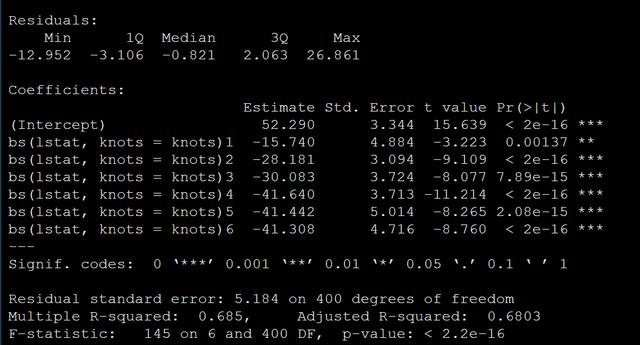
我們接著看廣義可加模型的R語言做法，我手上有數據如下：

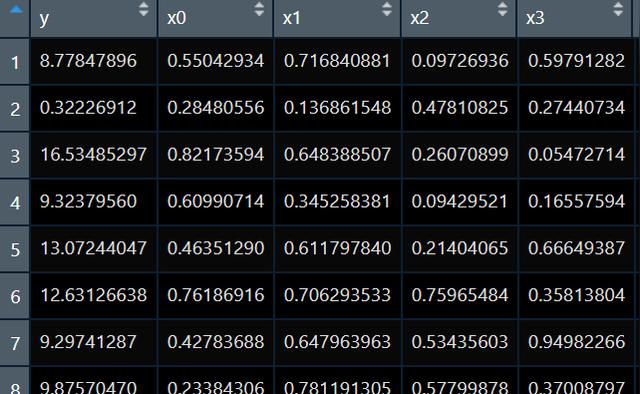
我現在想弄明白x3與y的關系，但是假如我現在已經知道，x1和x2與y的關系為非線性的，我們是不是要把這個非線性關系控制掉來看我們x3和y的關系呀。所以我們跑一個可加模型來瞅瞅：

b1 <- gam(y ~ s(x1, bs='ps', sp=0.6) + s(x2, bs='ps', sp=0.6) + x3, data = dat)summary(b1)

上面的代碼中bs設定平滑方法，sp設定λ。

運行上面的代碼后得到結果如下：

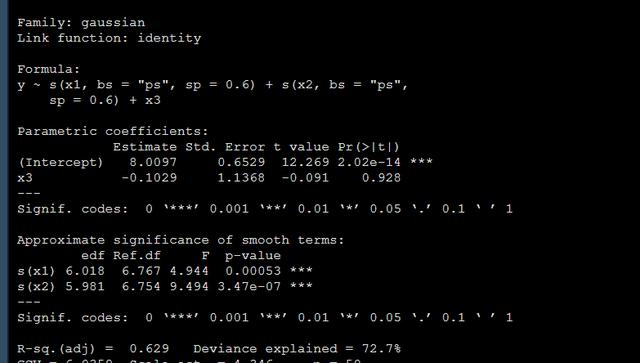
就是說在控制了x1和x2的曲線效應后，我們x3對y其實是沒有影響的。

小結

今天給大家寫了多項式回歸，樣條回歸和可加模型，希望能給到大家以啟發，感謝大家耐心看完，自己的文章都寫的很細，重要代碼都在原文中，希望大家都可以自己做一做，請轉發本文到朋友圈后私信回復“數據鏈接”獲取所有數據和本人收集的學習資料。如果對您有用請先記得收藏，再點贊分享。

也歡迎大家的意見和建議，大家想了解什么統計方法都可以在文章下留言，說不定我看見了就會給你寫教程哦，有疑問歡迎私信。

如果你是一個大學本科生或研究生，如果你正在因為你的統計作業、數據分析、模型構建,科研統計設計等發愁，如果你在使用SPSS, R，Python，Mplus, Excel中遇到任何問題，都可以聯系我。因為我可以給您提供最好的，最詳細和耐心的數據分析服務。

如果你對Z檢驗，t檢驗，方差分析，多元方差分析，回歸，卡方檢驗，相關，多水平模型，結構方程模型，中介調節，量表信效度等等統計技巧有任何問題，請私信我，獲取詳細和耐心的指導。

If you are a student and you are worried about you statistical #Assignments, #Data #Analysis, #Thesis, #Reports, #Composing, #Quizzes, Exams.. And if you are facing problem in #SPSS, #R-Programming, #Excel, Mplus, then contact me. Because I could provide you the best services for your Data Analysis.

Are you confused with statistical Techniques like z-test, t-test, ANOVA, MANOVA, Regression, Logistic Regression, Chi-Square, Correlation, Association, SEM, multilevel model, mediation and moderation etc. for your Data Analysis...??

Then Contact Me. I will solve your Problem...

加油吧，打工人！

往期精彩

R數據分析：用R語言做潛類別分析LCA

R數據分析：貝葉斯定理的R語言模擬

R數據分析：什么是人群歸因分數Population Attributable Fraction

R語言：利用caret的dummyVars函數設置虛擬變量

R數據分析：傾向性評分匹配完整實例（R實現）

R數據分析：有調節的中介

R數據分析：如何用R做驗證性因子分析及畫圖，實例操練

R數據分析：如何用R做多重插補，實例操練

R文本挖掘：中文詞云生成，以2021新年賀詞為例

R文本挖掘：中文文本聚類

R數據分析：臨床預測模型的樣本量探討及R實現

R數據分析：多分類邏輯回歸

R數據分析：列線圖的做法及解釋

R數據分析：混合效應模型實例

R數據分析：隨機截距交叉滯后RI-CLPM與傳統交叉滯后CLPM

R數據分析：生存分析的做法與解釋續

R數據分析：多水平模型詳細說明

R數據分析：如何做潛在剖面分析Mplus

R數據分析：競爭風險模型的做法和解釋二

R數據分析：多元邏輯斯蒂回歸的做法

R數據分析：探索性因子分析

R數據分析：層次聚類實操和解析，一看就會哦

R數據分析：交叉滯后模型非專業解釋

R數據分析：潛在剖面分析LPA的做法與解釋

R數據分析：中介作用與調節作用的分析與解釋

R數據分析：非專業解說潛變量增長模型

R數據分析：雙分類變量的交互作用作圖

R數據分析：如何給結構方程畫路徑圖，tidySEM包詳解

R數據分析：潛增長模型LGM的做法和解釋，及其與混合模型對比

R數據分析：結構方程模型畫圖以及模型比較，實例操練

R數據分析：混合效應模型的可視化解釋，再不懂就真沒辦法

R數據分析：結構方程模型的分組比較，實例解析

R數據分析：工具變量回歸與孟德爾隨機化，實例解析

R數據分析：潛類別軌跡模型LCTM的做法，實例解析

R數據分析：如何用層次聚類分析做“癥狀群”，實例操練