面試數據分析崗位的問題(數據科學的面試的一些基本問題總結)

2023-10-02

在這篇文章中，將介紹如何為成功的面試做準備的，以及可以幫助我們面試的一些資源。

代碼開發基礎

如果你是數據科學家或軟件開發人員，那么應該已經知道一些 Python 和 SQL 的基本知識，這對數據科學家的面試已經足夠了，因為大多數的公司基本上是這樣的——但是，在你的簡歷中加入 Spark 是一個很好的加分項。

對于 SQL，你應該知道一些最簡單的操作，例如：

從表中選擇某些列

連接兩個表（內連接、左連接、右連接和外連接）

匯總結果（總和、平均值、最大值、最小值）

在 SQL 中使用窗口函數

日期處理

對于 Python，需要了解：

處理df（pandas），例如讀取、加入、合并、過濾

操作日期和格式化日期

操作字符串，例如使用正則表達式、搜索字符串包含的內容

有效地使用循環

使用列表和字典

在 Python 中創建函數和類

在你的編程面試中，掌握 SQL 和 Python 是很重要的。

了解數據結構和算法

這是一個重要的問題，可能不像對軟件開發人員那么重要，但是對數據結構和算法有很好的理解肯定會讓你與眾不同。以下是一個好的開始：

大O符號

二進制搜索

數組和鏈表

選擇排序

快速排序

冒泡排序

合并排序

哈希表

下面進入本文的正題，將介紹一些基本的ML面試相關資料,可以作為筆記收藏

線性回歸

我關于線性回歸的大部分筆記都是基于《統計學習導論》這本書。

Logistic 回歸

它是一種廣泛使用的技術，因為它非常高效，不需要太多計算資源，高度可解釋，不需要縮放輸入特征，不需要任何調整，易于正則化，并且它輸出經過良好校準的預測概率。

與線性回歸一樣，當刪除與輸出變量無關的屬性以及彼此非常相似（相關）的屬性時，邏輯回歸的效果會更好。所以特征工程在邏輯和線性回歸的性能方面起著重要作用。 Logistic 回歸的另一個優點是，它非常容易實現并且訓練效率很高。我通常從邏輯回歸模型作為基準開始，然后嘗試使用更復雜的算法。

由于其簡單性以及可以相對容易和快速地實現的事實，邏輯回歸是一個很好的基準可以使用它來衡量其他更復雜算法的性能。

它的一個最主要的缺點是我們不能用它解決非線性問題，因為它的決策面是線性的。

邏輯回歸的假設：首先，邏輯回歸不需要因變量和自變量之間的線性關系。其次，誤差項（殘差）不需要服從正態分布。第三，不需要同方差性。最后，邏輯回歸中的因變量不是在區間或比率尺度上測量的。

但是，其他一些假設仍然適用。

首先，二元邏輯回歸要求因變量是二元的，而序數邏輯回歸要求因變量為序數。

其次，邏輯回歸要求觀察結果彼此獨立。換言之，觀察結果不應來自重復測量或匹配數據。

第三，邏輯回歸要求自變量之間很少或沒有多重共線性。這意味著自變量之間的相關性不應太高。

第四，邏輯回歸假設自變量和對數幾率是線性的。雖然這種分析不要求因變量和自變量線性相關，但它要求自變量與對數幾率線性相關。

最后，邏輯回歸通常需要大樣本量。對于模型中的每個自變量，一般情況下至少需要 10 個結果頻率最低的樣本。

聚類

使用 GMM 有兩個好處。首先，GMM 在集群協方差方面比 K-Means 靈活得多；由于標準偏差參數，簇可以呈現任何橢圓形狀，而不是僅限于圓形。 K-Means 實際上是 GMM 的一種特殊情況，其中每個集群在所有維度上的協方差都接近 0。其次，由于 GMM 使用概率，因此每個數據點可以屬于多個簇。因此，如果一個數據點位于兩個重疊集群的中間，我們可以簡單地定義它的類，方法是說它屬于類 1 的 X 百分比和屬于類 2 的 Y 百分比。

隨機森林和提升樹

這部分我們介紹的很多了，可以參考我門以前的文章：

自編碼器

自編碼器是一種無監督學習技術，利用神經網絡來完成表示學習的任務。具體來說，設計一個神經網絡架構，以便我們在網絡中包含一個瓶頸層（壓縮），強制原始輸入的壓縮知識表示。如果輸入特征彼此獨立，那么這種壓縮和隨后的重建將是一項非常困難的任務。但是如果數據中存在某種結構（即輸入特征之間的相關性），則可以學習這種結構，從而在強制輸入通過網絡瓶頸時加以利用。

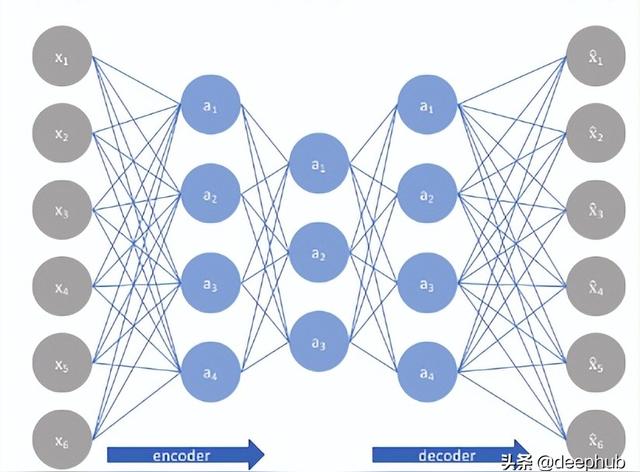
如上圖所示，我們可以將一個未標記的數據集構建為一個監督學習問題，其任務是輸出 x? ，即原始輸入 x 的重建。可以通過最小化重建誤差 (x,x? ) 來訓練該網絡，該誤差衡量我們的原始輸入與后續重建之間的差異。瓶頸層是我們網絡設計的關鍵屬性；在不存在信息瓶頸的情況下，我們的網絡可以很容易地學會通過網絡傳遞這些值來簡單地記住輸入值。

注意：事實上，如果我們要構建一個線性網絡（即在每一層不使用非線性激活函數），我們將觀察到與 PCA 中觀察到的相似的降維

因為神經網絡能夠學習非線性關系，這可以被認為是比 PCA 更強大的（非線性）泛化。 PCA 試圖發現描述原始數據的低維超平面，而自動編碼器能夠學習非線性流形（流形簡單地定義為連續的、不相交的表面）。

梯度下降

梯度下降是一種用于尋找可微函數的局部最小值的優化算法。梯度下降通過最小化成本函數的方法找到函數參數（系數）的值。這是一個迭代逼近的過程。

梯度只是衡量所有權重相對于誤差變化的變化。也可以將梯度視為函數的斜率。梯度越高，斜率越陡，模型學習的速度就越快。但是如果斜率為零，模型就會停止學習。在數學術語中，梯度是關于其輸入的偏導數。

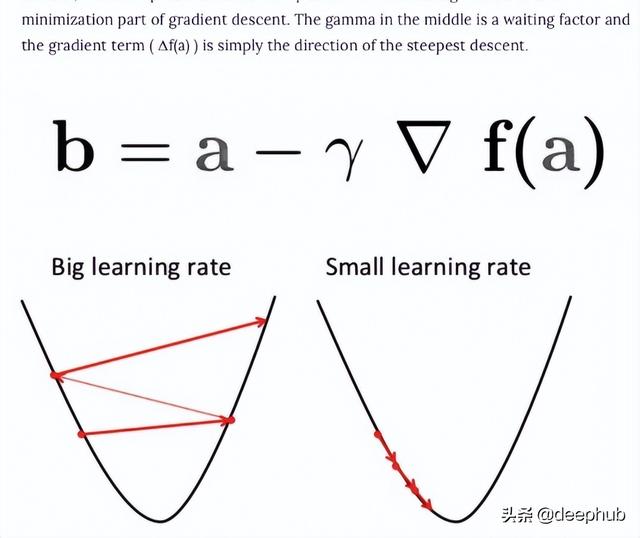
批量梯度下降：批量梯度下降，也稱為普通梯度下降，計算訓練數據集中每個示例的誤差，但只有在評估了所有訓練示例之后，模型才會更新。這整個過程就像一個循環，稱為一個訓練輪次。

批量梯度下降的一些優點是它的計算效率，它產生穩定的誤差梯度和穩定的收斂。缺點是穩定的誤差梯度有時會導致收斂狀態不是模型所能達到的最佳狀態。它還要求整個訓練數據集都在內存中并且可供算法使用。

隨機梯度下降：相比之下，隨機梯度下降 (SGD) 對數據集中的每個訓練示例執行此操作，這意味著它會一一更新每個訓練示例的參數。這可以使 SGD 比批量梯度下降更快。但是頻繁更新比批量梯度下降方法的計算成本更高。每一個樣本都計算梯度也會收到噪聲的影響，導致不是向著梯度的方向移動導致訓練時間的增加。

小批量梯度下降：小批量梯度下降是首選方法，因為它結合了 SGD 和批量梯度下降的概念。它只是將訓練數據集分成小批，并為每個批執行更新。這在隨機梯度下降的魯棒性和批量梯度下降的效率之間建立了平衡。

常見的 mini-batch 大小在 50 到 256 之間，但與任何其他機器學習技術一樣，沒有明確的規則，因為它因不同的應用程序而異。這是訓練神經網絡時的首選算法，也是深度學習中最常見的梯度下降類型。

獨熱編碼與標簽編碼

我們應該如何處理分類變量呢？事實證明，有多種處理分類變量的方法。在本文中將討論兩種最廣泛使用的技術：

標簽編碼

One-Hot 編碼

標簽編碼

標簽編碼是一種用于處理分類變量的流行編碼技術。在這種技術中，每個標簽都根據字母順序分配一個唯一的整數。

讓我們看看如何使用 scikit-learn 庫在 Python 中實現標簽編碼，并了解標簽編碼的挑戰。

第一列 Country 是分類特征，因為它由對象數據類型表示，其余的是數字特征，因為它們由 int64 表示。

# Import label encoder from sklearn import preprocessing # label_encoder object knows how to understand word labels. label_encoder = preprocessing.LabelEncoder() # Encode labels in column ‘Country’. data[‘Country’]= label_encoder.fit_transform(data[‘Country’]) print(data.head())

標簽編碼的問題

在上述場景中，國家名稱沒有順序或等級。但是很可能會因為數字本身導致模型很有可能捕捉到印度<日本<美國等國家之間的關系，這是不正確的。那么如何才能克服這個障礙呢？這里出現了 One-Hot Encoding 的概念

One-Hot 編碼

One-Hot Encoding 是另一種處理分類變量的流行技術。它只是根據分類特征中唯一值的數量創建附加特征。類別中的每個唯一值都將作為特征添加。

在這種編碼技術中，每個類別都表示為一個單向量。讓我們看看如何在 Python 中實現 one-hot 編碼：

# importing one hot encoder from sklearn from sklearn.preprocessing import OneHotEncoder # creating one hot encoder object onehotencoder = OneHotEncoder() #reshape the 1-D country array to 2-D as fit_transform expects 2-D and finally fit the object X = onehotencoder.fit_transform(data.Country.values.reshape(-1,1)).toarray() #To add this back into the original dataframe dfOneHot = pd.DataFrame(X, columns = [“Country_”+str(int(i)) for i in range(data.shape[1])]) df = pd.concat([data, dfOneHot], axis=1) #droping the country column df= df.drop([‘Country’], axis=1) #printing to verify print(df.head())

One-Hot Encoding 會導致虛擬變量陷阱，因為可以借助其余變量輕松預測一個變量的結果。

虛擬變量陷阱導致稱為多重共線性的問題。當獨立特征之間存在依賴關系時，就會發生多重共線性。多重共線性是線性回歸和邏輯回歸等機器學習模型中的一個嚴重問題。

因此，為了克服多重共線性問題，必須刪除其中虛擬變量。下面將實際演示在執行 one-hot 編碼后如何引入多重共線性問題。

檢查多重共線性的常用方法之一是方差膨脹因子 (VIF)：

VIF=1，多重共線性非常少

VIF<5，中度多重共線性

VIF>5，極端多重共線性（這是我們必須避免的）

最后說明：如果使用的樹型模型，使用標簽編碼就足夠了，使用線性模型建議還是使用獨熱編碼

超參數調優

隨機搜索交叉驗證

通常，我們對最佳超參數只有一個模糊的概念，因此縮小搜索范圍的最佳方法是評估每個超參數值。使用 Scikit-Learn 的 RandomizedSearchCV 方法，我們可以定義超參數范圍的網格，并從網格中隨機采樣，對每個值組合執行 K-Fold CV。

from sklearn.model_selection import RandomizedSearchCV# Number of trees in random forestn_estimators = [int(x) for x in np.linspace(start = 200, stop = 2000, num = 10)]# Number of features to consider at every splitmax_features = [‘auto’, ‘sqrt’]# Maximum number of levels in treemax_depth = [int(x) for x in np.linspace(10, 110, num = 11)]max_depth.append(None)# Minimum number of samples required to split a nodemin_samples_split = [2, 5, 10]# Minimum number of samples required at each leaf nodemin_samples_leaf = [1, 2, 4]# Method of selecting samples for training each treebootstrap = [True, False]# Create the random gridrandom_grid = {‘n_estimators’: n_estimators,‘max_features’: max_features,‘max_depth’: max_depth,‘min_samples_split’: min_samples_split,‘min_samples_leaf’: min_samples_leaf,‘bootstrap’: bootstrap}pprint(random_grid){‘bootstrap’: [True, False],‘max_depth’: [10, 20, 30, 40, 50, 60, 70, 80, 90, 100, None],‘max_features’: [‘auto’, ‘sqrt’],‘min_samples_leaf’: [1, 2, 4],‘min_samples_split’: [2, 5, 10],‘n_estimators’: [200, 400, 600, 800, 1000, 1200, 1400, 1600, 1800, 2000]}# Use the random grid to search for best hyperparameters# First create the base model to tunerf = RandomForestRegressor()# Random search of parameters, using 3 fold cross validation,# search across 100 different combinations, and use all available coresrf_random = RandomizedSearchCV(estimator = rf, param_distributions = random_grid, n_iter = 100, cv = 3, verbose=2, random_state=42, n_jobs = -1)# Fit the random search modelrf_random.fit(train_features, train_labels)

RandomizedSearchCV中最重要的參數是n_iter，它控制要嘗試的不同組合的數量，cv是用于交叉驗證的分折次數(我們分別使用100和3)。更多的迭代將覆蓋更大的搜索空間，更多的cv折疊將減少過擬合的機會，但提高每一個將增加運行時間。機器學習是一個權衡取舍的領域，性能與時間是最基本的權衡之一。

我們可以通過擬合隨機搜索來查看最佳參數:

rf_random.best_params_{‘bootstrap’: True,‘max_depth’: 70,‘max_features’: ‘auto’,‘min_samples_leaf’: 4,‘min_samples_split’: 10,‘n_estimators’: 400}

網格搜索交叉驗證

隨機搜索允許縮小每個超參數的范圍。也可以顯式地指定要嘗試的每個設置組合。使用GridSearchCV來實現這一點，該方法不是從一個分布中隨機抽樣，而是評估我們定義的所有組合。為了使用網格搜索，我們根據隨機搜索提供的最佳值創建另一個網格:

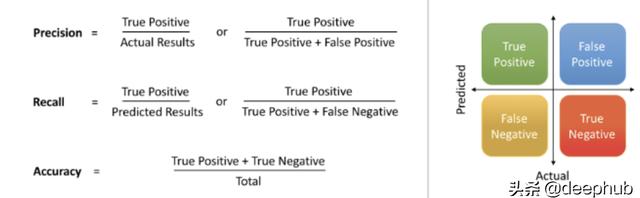
from sklearn.model_selection import GridSearchCV# Create the parameter grid based on the results of random searchparam_grid = {‘bootstrap’: [True],‘max_depth’: [80, 90, 100, 110],‘max_features’: [2, 3],‘min_samples_leaf’: [3, 4, 5],‘min_samples_split’: [8, 10, 12],‘n_estimators’: [100, 200, 300, 1000]}# Create a based modelrf = RandomForestRegressor()# Instantiate the grid search modelgrid_search = GridSearchCV(estimator = rf, param_grid = param_grid,cv = 3, n_jobs = -1, verbose = 2)

精度和召回

這些指標表示了模型在數據集中找到所有相關案例的能力

損失函數

回歸：

均方誤差損失

在數學上，如果目標變量的分布是高斯分布，則它是最大似然推理框架下的首選損失函數。首先要想到并且可以使直接使用損失函數，只有在有充分理由的情況下才建議使用其他的損失函數。

平均絕對誤差損失

在一些回歸問題中，目標變量的分布可能主要是高斯分布，但可能有異常值，例如平均值的大值或小值距離很遠。在這種情況下，平均絕對誤差或 MAE 損失是一個合適的損失函數，因為它對異常值更穩健。它被計算為實際值和預測值之間的絕對差的平均值

二元分類：

交叉熵：交叉熵將計算一個分數，該分數總結了預測類 1 的實際概率分布和預測概率分布之間的平均差異，完美的交叉熵值為 0。

Hinge Loss：

對于二元分類問題，交叉熵的替代方法是Hinge Loss，主要開發用于支持向量機 (SVM) 模型。它旨在與目標值在集合 {-1, 1} 中的二進制分類一起使用。Hinge Loss鼓勵示例具有正確的符號，當實際和預測的類值之間的符號存在差異時分配更多錯誤。Hinge Loss的性能報告是混合的，有時在二元分類問題上比交叉熵有更好的性能。

多類分類：多類交叉熵

最后總結

本文分享了一些在面試中常見的問題，后續我們還會整理更多的文章，希望這篇文章對你有幫助，并祝你為即將到來的面試做好準備!

作者：Sameen