二元邏輯回歸分析spss(Logistics回歸分析 之 二元邏輯回歸)
序曲
詠菊
【唐】白居易
一夜新霜著瓦輕,芭蕉新折敗荷傾。
耐寒唯有東籬菊,金粟初開曉更清。
【譯文】
一夜過后,初降的寒霜輕輕地附在瓦上,使得芭蕉折斷,荷葉傾倒。
耐寒的只有東邊籬笆旁的菊花,它花蕊初開,讓早晨多了一份清香。
【賞析】
初降的霜輕輕的附著在瓦上,芭蕉和荷花無法耐住嚴寒,或折斷,或歪斜,惟有那東邊籬笆附近的菊花,在寒冷中傲然而立,金粟般的花蕊初開讓清晨更多了一絲清香。
夜里寒霜襲來,本來就殘破的芭蕉和和殘荷看起來更加不堪。只有籬笆邊的菊花,金黃色的花朵在清晨的陽光下看起來更加艷麗。用霜降之時,芭蕉的新折和荷葉的殘敗來反襯東籬菊的清絕耐寒。此詩贊賞菊花凌寒的品格。
整詩是借詠菊之耐寒傲冷逸清香亮霜景,自況言志的。
二元邏輯回歸分析
二元邏輯回歸是指因變量為二分類變量的回歸分析。在建回歸模型時,目標概率的取值在0~1之間,但回歸方程的因變量取值卻落在實數集中,這是不能接受的。因此,可以先將目標概率做Logit變化,取值區間就變成了整個實數集,再做回歸分析即可。
優勢比(odds)
把出現某種結果的概率與不出現的概率之比稱為比值(Odds),即Odds=P/(1-P),兩個比值之比也為比值比,也稱為優勢比(Odds Ratio,OR),優勢比是反映兩個二項分類變量之間關系的指標。
具體研究如下表所示,研究某項因素的暴露是否對某種疾病的發生有影響,總的暴露優勢為:
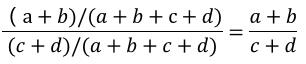
病例的暴露優勢為:
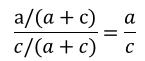
對照的暴露優勢為:
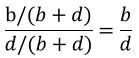
病例與對照的暴露優勢比為:
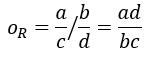
如果a/b/c/d分別為30,20,50,50,則優勢比OR = (30*50)/(50*20) = 1.5,即病例暴露優勢是對照的1.5倍。

邏輯回歸系數的意義
依據公式,邏輯回歸方程可定義為:
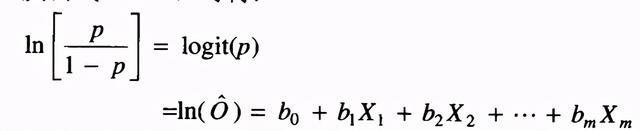
類似于線性回歸系數的解釋,在邏輯回歸方程中,回歸系數bj表示其他自變量固定不變的情況下,某一自變量Xj改變一個單位logit(p)或對數優勢的平均該變量。
但在實際工作中,邏輯回歸不是直接解釋回歸系數bj,而是解釋優勢比。優勢比被用來作為效應大小的指標,度量某自變量對因變量優勢影響程度的大小。某一自變量Xj對應的優勢比為:ORj=exp(bj)
優勢比的含義是:在其他自變量固定不變的情況下,某一自變量Xj改變一個單位,因變量對應的優勢比評價改變exp(bj)各單位。
之前也談到過,自變量可以是無序或有序多項分類變量、二項分類變量、連續變量。上面提到的優勢比是連續變量的優勢比含義。對于無序多分類變量,需要進行啞變量化(后續會進行講解)。如果有k個分類,則需產生k-1個啞變量,每一個啞變量的優勢比是相對于參考分類,因變量優勢的平均改變量。
如果進行發病或死亡的危險因素研究,那么
當bj>0,即bj為正數時,ORj=exp(bj) 大于1,說明該因素是危險因素;
當bj<0,即bj為負數時,ORj=exp(bj) 小于1,說明該因素是保護因素;
當bj=0,即ORj=exp(bj) =1,說明該因素與因變量無關。
標準化回歸系數
由于不同的變量其相應的度量衡單位可能不同,不能采用偏回歸系數的絕對值大小來比較各個自變量的相對作用大小,為此需要引入標準化邏輯回歸系數。
注意:標準化邏輯回歸系數只是一個相對大小值,主要通過它的絕對值大小來比較不同自變量對模型的貢獻大小,而不用于構建回歸模型,構建回歸模型需要采用一般的回歸系數。
標準化回歸系數估計可采用以下公式:
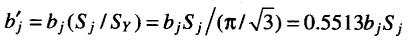
其中:bj是一般的回歸系數,即偏回歸系數;Sj為第j自變量的標準差。
在SPSS中沒有提供計算選項,需要通過 轉換-計算變量 來進行計算。
啞變量定義
啞變量(DummyVariable),也叫虛擬變量, 引入啞變量的目的是,將不能夠定量處理的變量量化,在回歸分析中引入啞變量的目的是,可以考察定性因素對因變量的影響。
啞變量是人為虛設的變量,通常取值為0或1,來反映某個變量的不同屬性。對于有n個分類屬性的自變量,通常需要選取1個分類作為參照,因此可以產生n-1個啞變量。
如職業、性別對收入的影響,戰爭、自然災害對GDP的影響,季節對某些產品(如冷飲)銷售的影響等等。這種“量化”通常是通過引入“啞變量”來完成的。根據這些因素的屬性類型,構造只取“0”或“1”的人工變量,通常稱為啞變量(dummyvariables),記為D。
舉一個例子,假設變量“職業”的取值分別為:工人、農民、學生、企業職員、其他,5種選項,我們可以增加4個啞變量來代替“職業”這個變量,分別為D1(1=工人/0=非工人)、D2(1=農民/0=非農民)、D3(1=學生/0=非學生)、D4(1=企業職員/0=非企業職員),最后一個選項“其他”的信息已經包含在這4個變量中了,所以不需要再增加一個D5(1=其他/0=非其他)了。這個過程就是引入啞變量的過程。
SPSS實現二元邏輯回歸分析
示例:醫生研究了出生低體重嬰兒的影響因素,因變量為是否出生低體重兒(變量名為Low,1-是,0-否),希望篩選出出生低體重兒的影響因素,考慮因素:產婦妊娠前體重、產婦年齡、產婦在妊娠期間是否吸煙、種族等。
打開 分析—回歸—二元Logistic
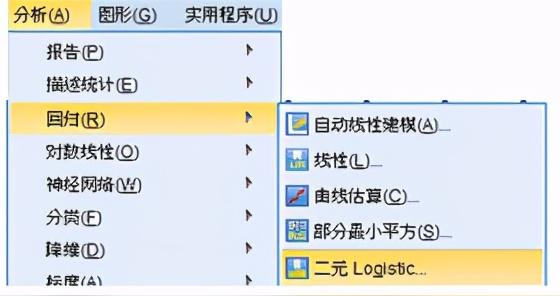
2.參數選擇與說明
(1)主頁面
因變量:從變量列表中選擇一個二分類變量作為因變量,可以是數值型變量或短字符型變量。
協變量:從變量列表中選擇自變量,可以選入單個變量,還可以選入變量之間的交互項,方法是在變量類別同時選中多個變量后,單擊 >a*b>按鈕,這些選中變量的所有交互作用就被選中。
方法:本例選擇 向前步進法(似然比)
--輸入 Enter:強迫進入法,所選自變量全面放在模型中,默認選項
--Forward-Conditinal:向前逐步法(條件似然比),變量引入的依據是統計量的顯著性水平;剔除的依據是條件參數估計所得的似然比統計量的概率值
--Forward-LR:向前逐步法(似然比),變量引入的依據是統計量的顯著性水平;剔除的依據是最大偏似然估計所得的似然比統計量的概率值
--Forward-Wald:向前逐步法(瓦爾德),變量引入的依據是統計量的顯著性水平;剔除的依據是 Wald統計量的概率值
--Backward-Conditinal:向后逐步法(條件似然比),變量剔除的依據是條件參數估計所得的似然比統計量的概率值
--Backward-LR:向后逐步法(似然比),剔除的依據是最大偏似然估計所得的似然比統計量的概率值
--Backward-Wald:向后逐步法(瓦爾德),剔除的依據是 Wald統計量的概率值
選擇變量:選擇一個變量,根據該變量的值,通過右側的規則按鈕,建立選擇條件
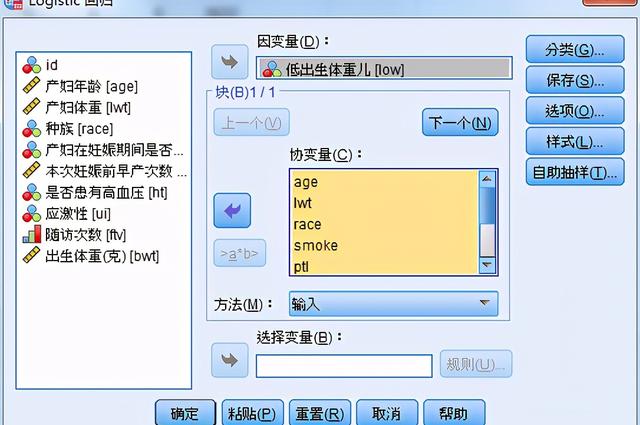
(2)分類 頁面
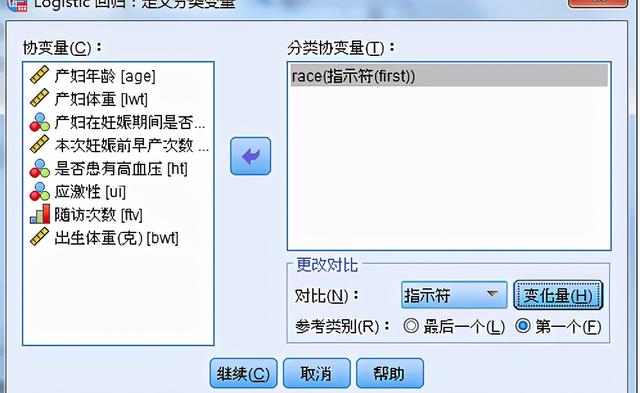
設置分類變量啞變量;若自變量為多分類變量,由于多分類自變量與因變量之間一般不存在線性關系,需要用啞變量分析,系統自動產生k-1個啞變量
更改對比:選擇分類變量的各水平的對照方式
Indicator指示符:指示是否屬于某一個分類,參考分類在對比矩陣中整行為0
Simple 簡單比較:預測變量的滅個分類都與參考分類進行比較
Difference 差分比較:除第一類外,預測變量的每個分類都與其前所有分類的平均效應進行比較
Helmert比較:除最后一類外,預測變量的每個分類都與后面所有分類的平均效應進行比較
Repeated重復比較:除第一類外,預測變量的每個分類都同其前的所有類別進行比較
Polynominal多項式比較:假設各類別的間距相等,適用于數值型變量
Deviation差別比較:預測變量的每個分類都同總體效應比較
參考類別:選擇Deviation、simple、indicator方法,需指定 1 個參考類別
默認是最后一個為參考類別
第一個:選擇第一個作為參考類別
(3) 保存 頁面

預測值:保存模型的預測值
預測值-概率:事件發生的預測概率
預測值-組成員:預測分類,根據預測概率得到的每個樣本的預測分類
影響:設置保存對單個觀測記錄進行預測時的影響力指標
庫克距離:表示把一個個案從計算回歸系數的樣本中去除時所引起的殘差變化的大小,距離越大,表明該個案對回歸系數的影響也越大
杠桿值:衡量的那個觀測 對回歸效果的影響程度,取值在0-n/n-1之間,取0時表示當前記錄對模型的擬合無影響
DfBeta:剔除一個個案后回歸系數的改變
殘差:
Unstandardized 非標準化殘差:觀察值與模型預測值之差
Logit 邏輯殘差:殘差除以“預測概率×(1-預測概率)”
Studentized 學生化殘差:用殘差除以關于殘差標準差的估計值,取決于當前個案自變量的取值與自變量均值之間的距離
Standardized 標準差殘差:均值為0,標準差為1
Deviance 變異殘差:基于模型變異的殘差
(4)選項 頁面
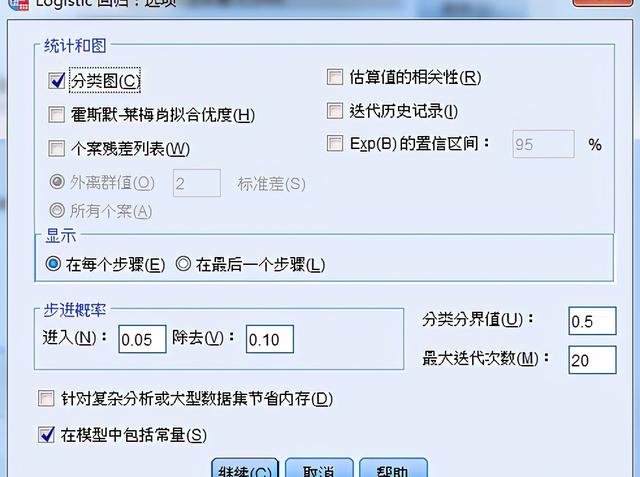
統計與圖:輸出統計量和圖形
分類圖:因變量的預測值與觀測值的分類直方圖
霍莫斯-萊梅肖擬合優度:比傳統邏輯回歸分析的擬合優度更穩定,特別是對含有連續型協變量模型和小樣本的研究
個案殘差列表:包括非標準化殘差、預測概率、觀測量的實際與預測分組水平
估算值的相關性:輸出參數估計值的相關系數矩陣
迭代歷史記錄:輸出每一步迭代的相關系數和對數似然比
Exp(B)的置信區間:輸入框指定1-99的數值
顯示:
每個步驟:表示在每一步迭代過程輸出相關表格、統計量和圖形
最后一個步驟:表示只輸出與最終方差有關的表格、統計量和圖形
分類分界值
指定對觀察量進行預測分類的臨界值
預測值大于指定值的觀測值被歸于一類,其余觀測量歸于量一類
結果輸出與解釋
(1) 基本描述
下圖給出樣本數、缺失樣本數、啞變量編碼以及因變量編碼
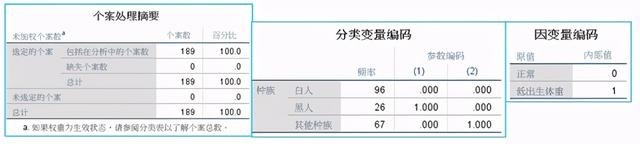
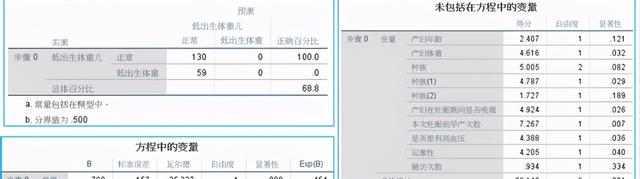
(2)Step0:自變量沒有選入,只有常數的情況
依據P值可看出下一步選入哪個變量
瓦爾德=25.327,p=0.000<0.05,顯著性差異
從分類表上看,選擇樣本的邏輯回歸模型對正常體重的預測準確率為100%,但對低出生體重預測準去率為0%,由此模型不可靠。
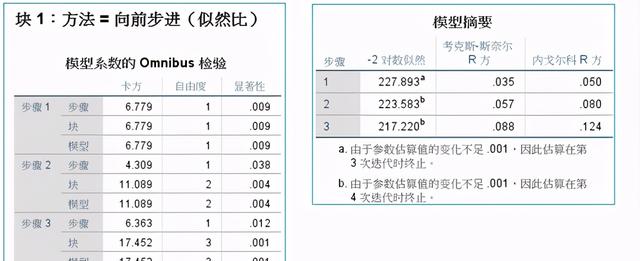
(3)模型摘要
在步驟三中的模型的p=0.000,基于該模塊建立的模型非常顯著
在步驟三中的R2為0.088,模型擬合效果較差
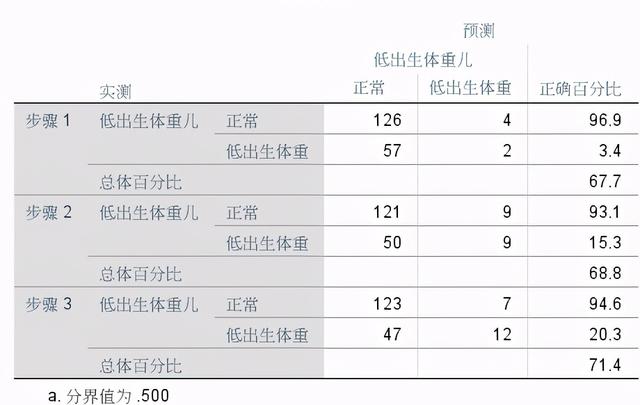
(4)分類表
從步驟1到步驟3,總體正確率百分比逐漸升高,在步驟3中正確率為71.4%
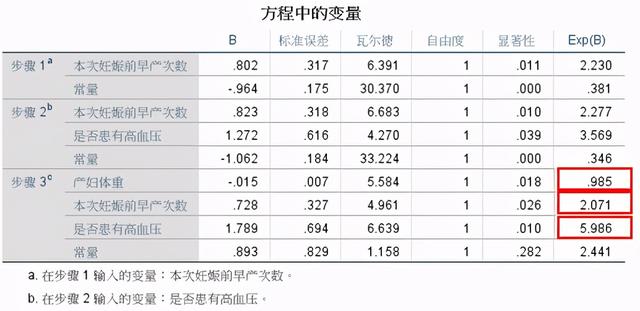
(5)方程中的系數
患有高血壓的孕婦所出生的低體重嬰兒是無高血壓孕婦的5.986倍;
體重的exp=0.985,在其他因素不變的情況下,體重增加1kg,出生低體重嬰兒的優勢比為0.985,表明體重增加出生低體重嬰兒有減少趨勢;
早產次數exp=2.071,表明早產增加1次,出生低體重嬰兒的比例增加2.071倍。
4.語法
******************** 二元邏輯回歸 ******************.LOGISTIC REGRESSION VARIABLES low/METHOD=FSTEP(LR) age lwt race smoke ptl ht ui ftv/CONTRAST (race)=Indicator(1)/SAVE=PRED PGROUP RESID/CLASSPLOT/CRITERIA=PIN(0.05) POUT(0.10) ITERATE(20) CUT(0.5).