stata回歸中虛擬變量為自變量(CFA教材詳解:在回歸中使用虛擬變量(Dummy Variables))
更多CFA官方教材詳解,請關注“邊際實驗室”。
“邊際實驗室”是一家專注于金融科技、金融大數據領域的工作室,同時提供CFA、FRM等金融考試內容的免費講解。
通常,分析師在回歸分析中需要使用定性變量作為自變量。有一種類型的定性變量,稱為虛擬變量,如果特定條件為真,則取值為1;如果條件為假,則取值為0。例如,假設我們要檢驗一月份的股票收益是否與剩余月份不同。我們在回歸中納入一個自變量X1t,該變量對應每年一月份的取值為1,對于一年中的其他月份的取值為0。我們估計回歸模型
Yt= b0 + b1X1t +εt
在該等式中,系數b0是除1月份以外的月份中的Yt的平均值,b1是1月份的Yt的平均值與1月份以外的月份中的Yt的平均值的差。
我們需要謹慎選擇回歸中虛擬變量的數量。規則是,如果要區分n個類別,則需要n-1個虛擬變量。例如,為了區分一月和一月以外的月份(n= 2個類別),我們使用一個虛擬變量(n-1= 2-1 =1)。如果要區分一年中的每個季度,我們將使用三個虛擬變量。如果我們錯誤地選擇了四個虛擬變量,這樣就違反了多元回歸模型的假設2,因此無法對回歸進行估計。以下案例說明了在使用每月數據進行回歸時使用虛擬變量的情況。
案例 對日本小盤股票收益的月度影響
多年來,分析師一直關注股票收益的季節性。特別是,分析師研究了一年中不同月份的小盤股票的收益是否不同。假設我們要檢驗一個小盤股票指數(MSCI日本小盤股指數)的總回報是否因月份而異。使用2001年1月到2013年底的數據,我們可以估算出包括截距和11個虛擬變量的回歸,每個變量分別對應于一年的前11個月。我們估計的方程為t= b0 + b1Jant + b2Febt +…+ b11Novt +εt。
其中,每個月的虛擬變量在發生月份時的值為1(例如,Jan1= Jan13 = 1,因為第一個觀察值為1月),而其他月份的值為0。下圖顯示了回歸的結果。
截距b0衡量12月時股票平均收益,因為12月沒有虛擬變量。此等式估計12月的平均收益為2.73%(^b0=0.0273)。虛擬變量的每個估計系數都顯示該月的收益與12月的收益之間估計的差值。因此,例如,一月份的估計收益比12月低2.13%(^b1=–0.0213)。
這樣得出的一月回報預測為0.60%(12月為2.73,對應于一月為2.13)。
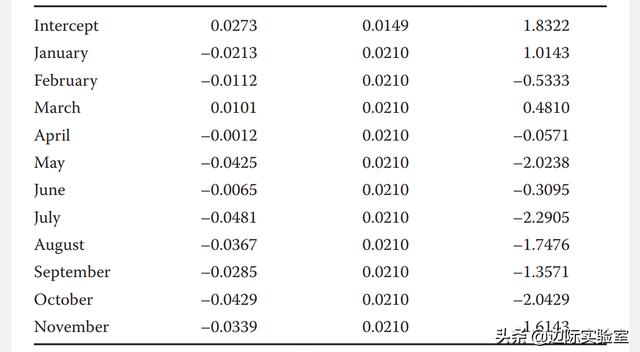
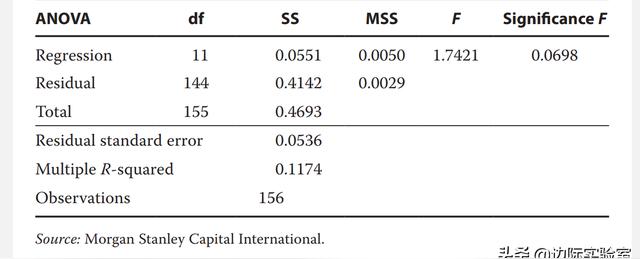
但是,此回歸的低R2(0.1174)表明,月度效應對于解釋小盤股票收益率可能不是很重要。我們可以使用F檢驗來分析原假設,即每月虛擬變量都等于0(H0:b1= b2 = ... = b11 = 0)。我們檢驗小盤股票收益率的每月顯著變化。上圖顯示了進行方差分析所需的數據。F檢驗分子的自由度數為11;分母中的自由度數為[156-(11+ 1)]=144。回歸平方和等于0.0551,殘差平方和等于0.4142。因此,確定所有回歸斜率系數是否都等于0的F統計量為
(0.0551/ 11)/( 0.4142 / 144) = 1.74
然后我們查閱F分布表得出F檢驗的結果。如果我們選擇0.05的顯著性水平并查看第11列(因為分子具有11個自由度),則我們看到當分母具有120個自由度時,臨界值為1.87。分母實際上具有144個自由度,因此F統計量的臨界值小于1.87(df= 120)但大于1.79(無限多個自由度)。檢驗統計量的值為1.74,因此我們不能拒絕原假設,即所有系數共同等于0。
圖表中顯示F檢驗的p值為0.0698,這意味著我們可以拒絕原假設的最小顯著性水平大約為0.07,即7%,高于5%的常規水平。在11個每月的虛擬變量中,5月、7月和10月的t統計量的絕對值大于2。盡管這些虛擬變量的系數在統計上是顯著的,但是我們有很多無關緊要的估計系數,因此我們不能拒絕每個月回報相等的原假設。該檢驗表明,回歸模型中一些系數的顯著性可能是隨機變化的結果。因此,我們可能希望避免要求在不同月份中對小型股票使用不同投資權重的投資組合策略。
案例 中國公司并購中短期股票收益表現的決定因素
Bhabra和Huang(2013)研究了上海證券交易所和深圳證券交易所上市的中國公司發起的并購交易的短期市場反應。他們研究了1997年至2007年期間收購方完全控制被收購目標的交易。作為衡量公告日前后短期股票收益表現的指標,他們使用了從–2天到+2天的5天的時間窗口內,并購者股票的累計異常收益,其中第0天是收購公告日。累積異常收益是在給定期間內相對于給定證券風險預期收益衡量的超額收益。模型中的獨立變量包括以下與公司和交易有關的因子,這些因子可能會影響短期股票收益率的表現:
■利潤率:收購前收購方的凈利潤與收入之比;
■銷售增長:收購前收購方的年銷售增長率;
■杠桿率變化:由于收購而導致的收購方債務與總資產之比的變化;
■公司價值:公告年度收購方市值的自然對數;
■是否同一行業:虛擬變量(1=收購方和目標公司位于同一行業,0=不同行業);
■是否國有企業:虛擬變量(1=收購公司是國有公司,0=不是國有公司);
■是否現金并購:虛擬變量(1=交易中的付款方式為現金,0=其他付款方式);
■是否跨境交易:虛擬變量(1=跨境交易,0=國內交易);
■目標公司是否私人企業:虛擬變量(1=目標公司是獨立的私人企業,0=不是獨立的私人企業);
■付款方式是否可獲取:虛擬變量(1=無法從公開信息中獲取付款信息形式,0=可獲取付款信息形式)。
下圖顯示了結果。
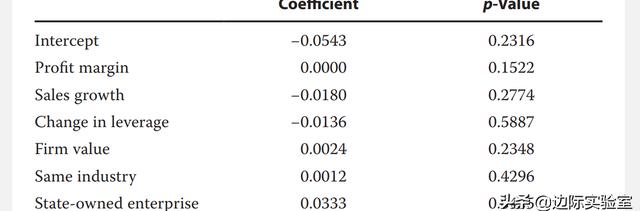
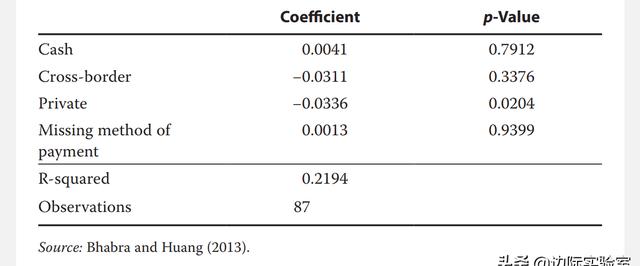
我們可以將該研究的發現總結如下:
■在此回歸模型中,是否國有企業的系數為正,在p值小于0.05的情況下,在0.05的置信水平上具有統計學意義。國有企業在中國經濟中扮演著非常重要的角色,非國有企業相對國有企業來講普遍較小。國有企業的系數具有統計上的顯著意義表明,當收購方為國有企業時,企業市值在短期增長的可能性更大。
■目標公司是否私人企業的系數在0.05的置信水平上也具有統計學意義。該系數的符號為負。這說明與收購上市公司的子公司相比,目標為私人企業往往會更低的異常收益。作者認為,由于私人企業的財務狀況相對不透明,在收購方在估計其價值和前景時面臨挑戰,因此引起更消極的股價反應。
盡管以上模型中其他系數均無統計學意義,但在研究中使用的其他模型中,作者發現一些證據表明,當目標企業與收購方行業一致以及杠桿率較低時,股票價格的反應更為積極。
文/邊際實驗室,轉載請務必注明出處

